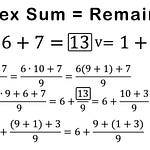YouTube - Summary - Notes - Playlist - MES Science playlist
In this video I show that not only is the vortex sum (summing of digits a number until 1 digit remains) is the remainder when dividing by the largest single digit, but this same number repeats indefinitely after the decimal place. For example, 67 v= 6 + 7 = 13 v= 1 + 3 = 4, and 67/9 = 7.44444..., where the remainder is 4/9 and the repeating digit is 0.4444... This is in fact the same for any number system when dividing by the highest single digit. I show that this is due to the infinite loop that arises when dividing by the highest single digit of any number system, since the number after it is always the transition number 10. Fascinating stuff!
#math #vortexmath #modulararithmetic #algebra #education
Timestamps
Division by Largest Unique Digit Repeats digits and equals vortex sum – 0:00
Repeating digit is a result of dividing by the highest single digit of any number system – 0:43
Continuous loop of division = repeating digit – 3:07
Works for any number – 5:40
Works for any base, including Base 5 – 6:32
In general for Base p: 1/p = 0.1111... etc. – 9:11
MES Convention: Vortex Sum is repeating digit sums until we obtain 1 digit – 9:54