YouTube - Summary - Notes - Playlist - MES Science playlist
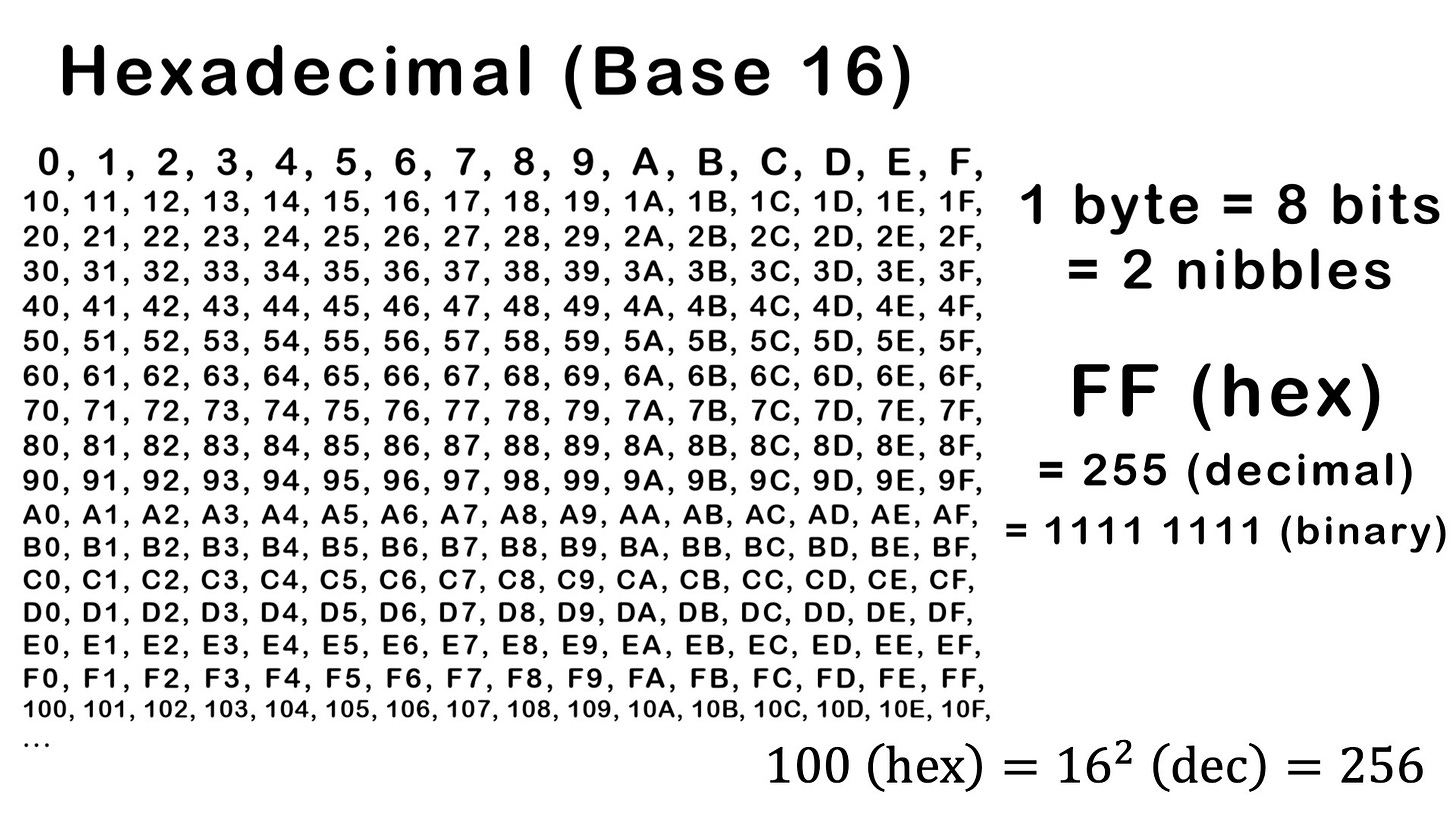
In this video I go over the hexadecimal (or base sixteen) number system and show how to convert it to binary (base two) and decimal (base ten). The hex (for short) system involves 16 single digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F) which includes a combination of numbers and letters. As usual, the number “10” represents the transition number, so 10 (hex) is the equivalent to 16 (dec) = 2^4 (dec) or 1111 (binary). This is particular useful for condensing binary numbers into shorter digits. For example, 1 byte is 8 digits of 1s and 0s, from 0000 0000 to 1111 1111 (binary), and can be condensed to just 2 “nibbles” or digits 00 to FF (hex) — in decimal, this would be from 0 to 256. As such, hexadecimals are used often in computing to simplify and condense binary digits.
#math #binary #hexadecimal #decimal #education
Timestamps
Example 3: Base 16 (Hexadecimal or Hex) number system: 0 to 9 and A to F https://en.wikipedia.org/wiki/Hexadecimal – 0:00
Number “10” is once again a transition number – 0:31
Base Two to Base Ten to Base Sixteen: 1 Byte = 8 Bits = 8 Binary digits – 1:31
1111 1111 (binary) = 255 (decimal) – 2:19
100 (Hex) = 16^2 (base 10) = 256 – 4:17
1 byte = 8 bits = 0000 000 to 1111 1111 (binary) = 0 to 255 (decimal) = 0 to FF (hex) – 6:00