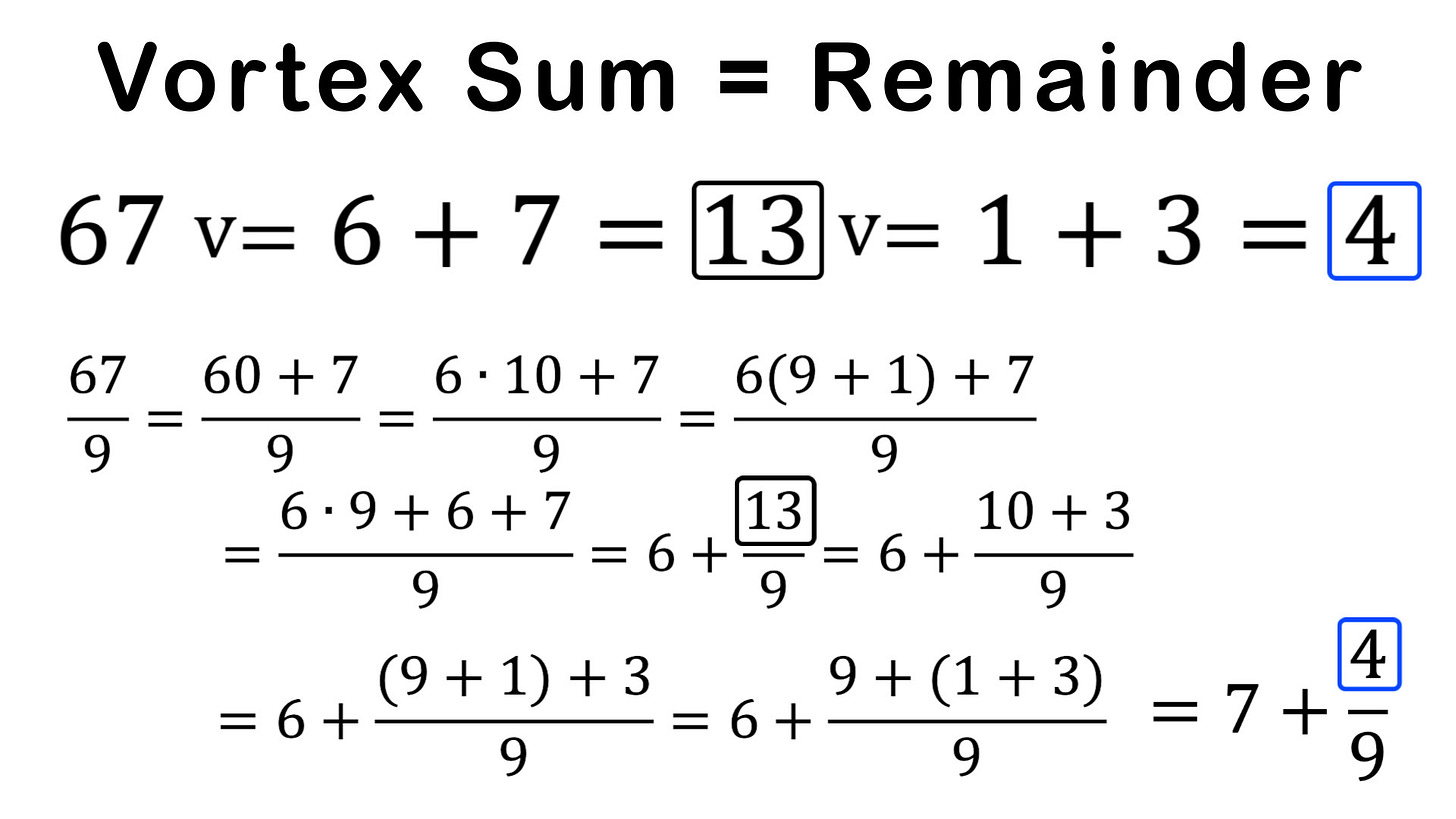YouTube - Summary - Notes - Playlist - MES Science playlist
In this video I show that the “vortex sum” of a number (summing up the digits until obtaining a single digit is obtained) is just the remainder when dividing the number by 9. I go over a couple of examples while also illustrating why this is the case by writing the transition numbers 10, 100 as (9 + 1), (99 + 1). I will prove this is always the case when in later videos when I cover the modulo function. Note that I denote “v=” when taking the vortex sum.
#math #vortexmath #modulararithmetic #algebra #education
Timestamps
Summing integer digits and the remainder after division. “v=” = “vortex sum” – 0:00
11 = 10 + 1 = (9 + 1) + 1 = 9 + (1 + 1) = 9 + 2 – 0:55
Dividing 11 by 9 we get 1.222... – 1:32
The 2 is the remainder – 2:55
678 v= 6 + 7 + 8 = 21 v= 2 + 1 = 3. 678/9 = 75.333... – 3:25
Deriving in MES fraction form, separating transition “10” numbers into “9 + 1” – 4:10
Factoring out the 9s in the denominator – 6:10
Repeat division of 21/9 – 8:15
Remainder is always the same as the vortex sum – 10:41