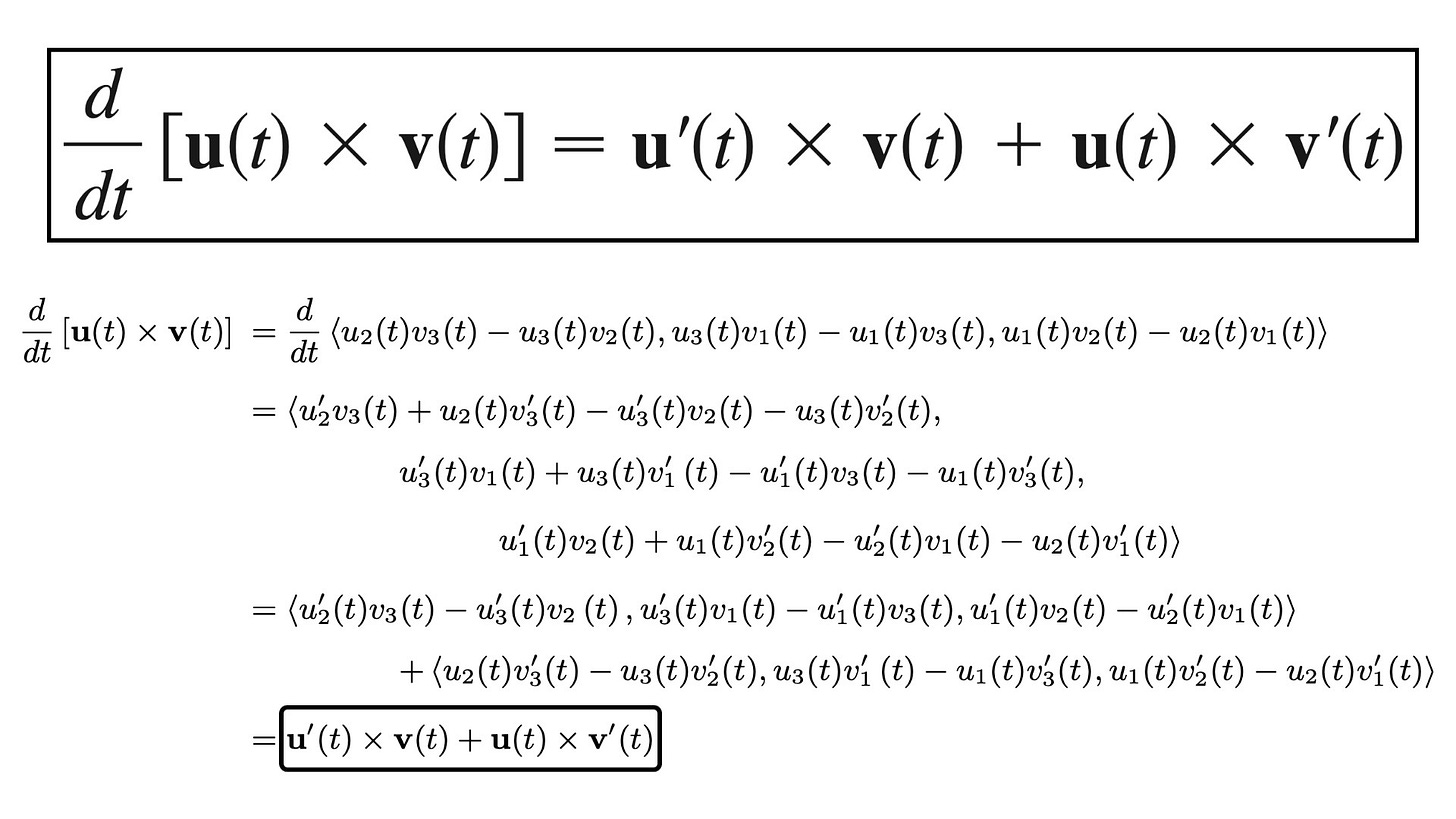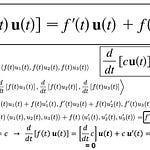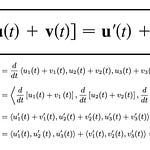YouTube - Summary - Notes - Playlist - Vector Functions playlist
In this video I prove Formula 5 of the differentiation rules for vector functions, and this time derive the derivative of the cross product of two vector functions. I solve this by taking the derivative of the components of the cross product directly and then separating it into two vectors. The result is the usual counterpart of the product rule for real-valued functions. In the next video I solve Formula 5 using the definition of derivative for vector functions instead.
#math #vectors #calculus #crossproduct #education
Timestamps
Exercise 5: Proof of Formula 5: Derivative of Cross Product: 0:00
Solution 1: Derivative of Components: 0:39
Expanding the cross product first: 2:26
Take derivative via product rule for each component: 4:49
Factor out all the similar terms to obtain two vectors: 7:48
Separate into two cross products: 11:53
We obtain our product rule counterpart for the derivative of cross product of vector functions: 14:11