YouTube - Summary - Notes - Playlist - Vector Functions playlist
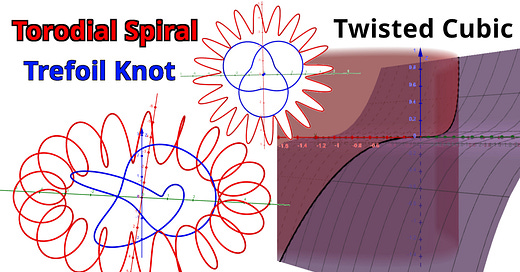
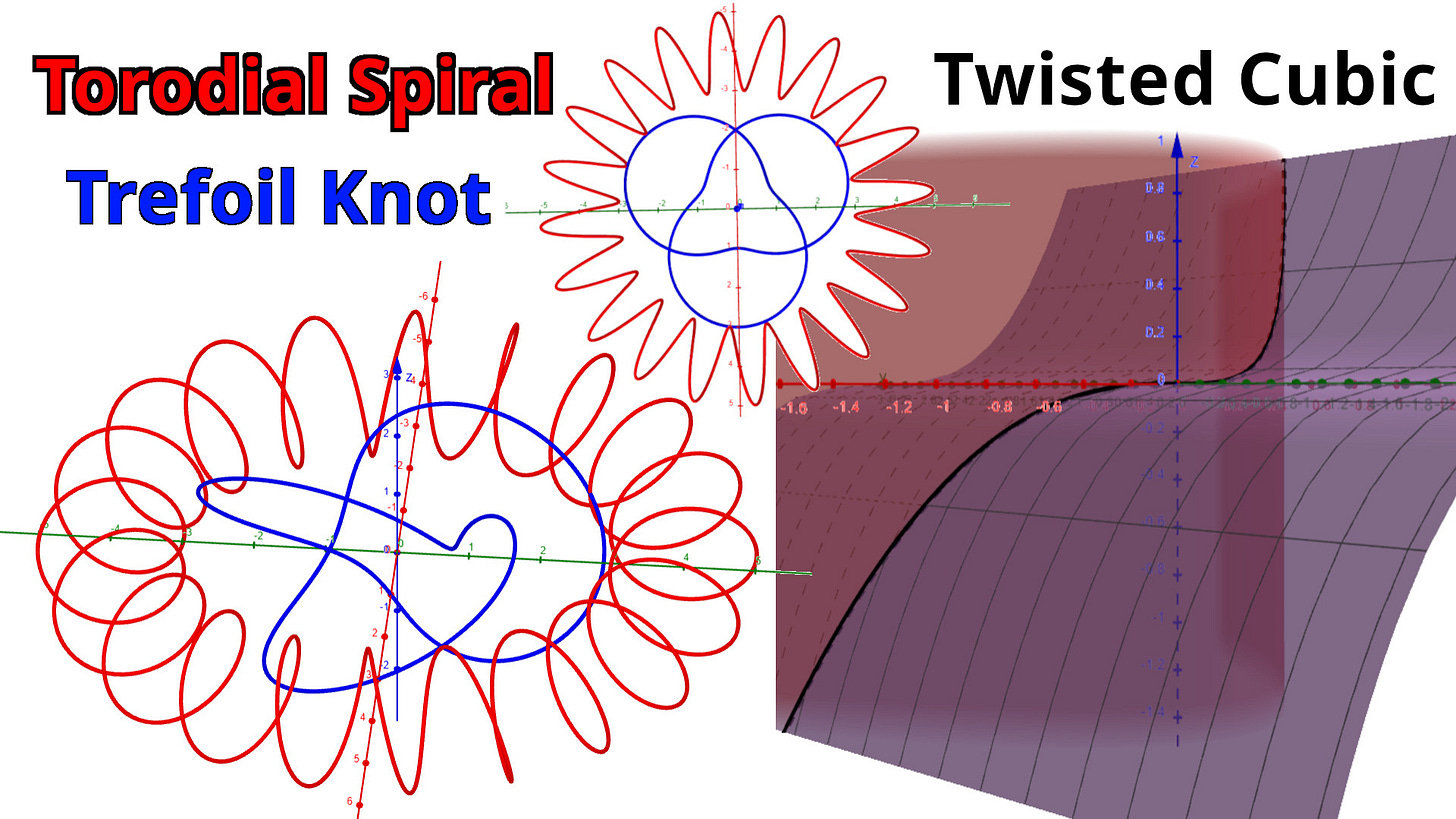
In this video I graph out several complicated space curves using GeoGebra's amazing 3D graphing calculator. These curves are the toroidal spiral, trefoil knot, and a twisted cubic. I illustrate the importance of perspective when viewing these three dimensional curves, by graphing the projections along each major coordinate plane. I also show that we can better visualize space curves by graphing them on 3D surfaces. For example, the twisted cubic is just the intersection curve between a parabolic and cubic cylinder!
#math #3D #spacecurves #GeoGebra #calculator
Timestamps
Example 7: Space curves are more difficult to draw than plane curves: 0:00
Toroidal spiral: 0:31
Trefoil knot: 1:06
Graphing the Trefoil knot and Toroidal spiral in GeoGebra: https://www.geogebra.org/calculator/gyfv87f2 1:33
Example 7: Twisted Cubic: 3:13
Views of the Twisted Cubic: 7:03
Twisted Cubic in GeoGebra: https://www.geogebra.org/calculator/vxv5heat 7:28
Visualizing Space Curves on Surfaces: 8:37
Twisted cubic on a parabolic cylinder: 9:46
Graphing Twisted Cubic on the intersection of two cylinders in GeoGebra: 11:18








Share this post