YouTube - Summary - Notes - Playlist - Vector Functions playlist
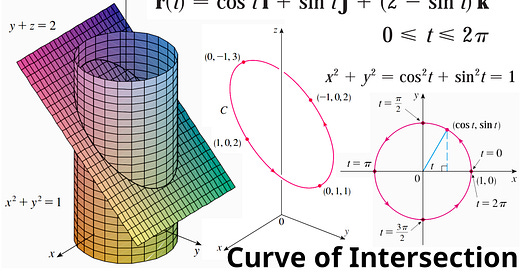
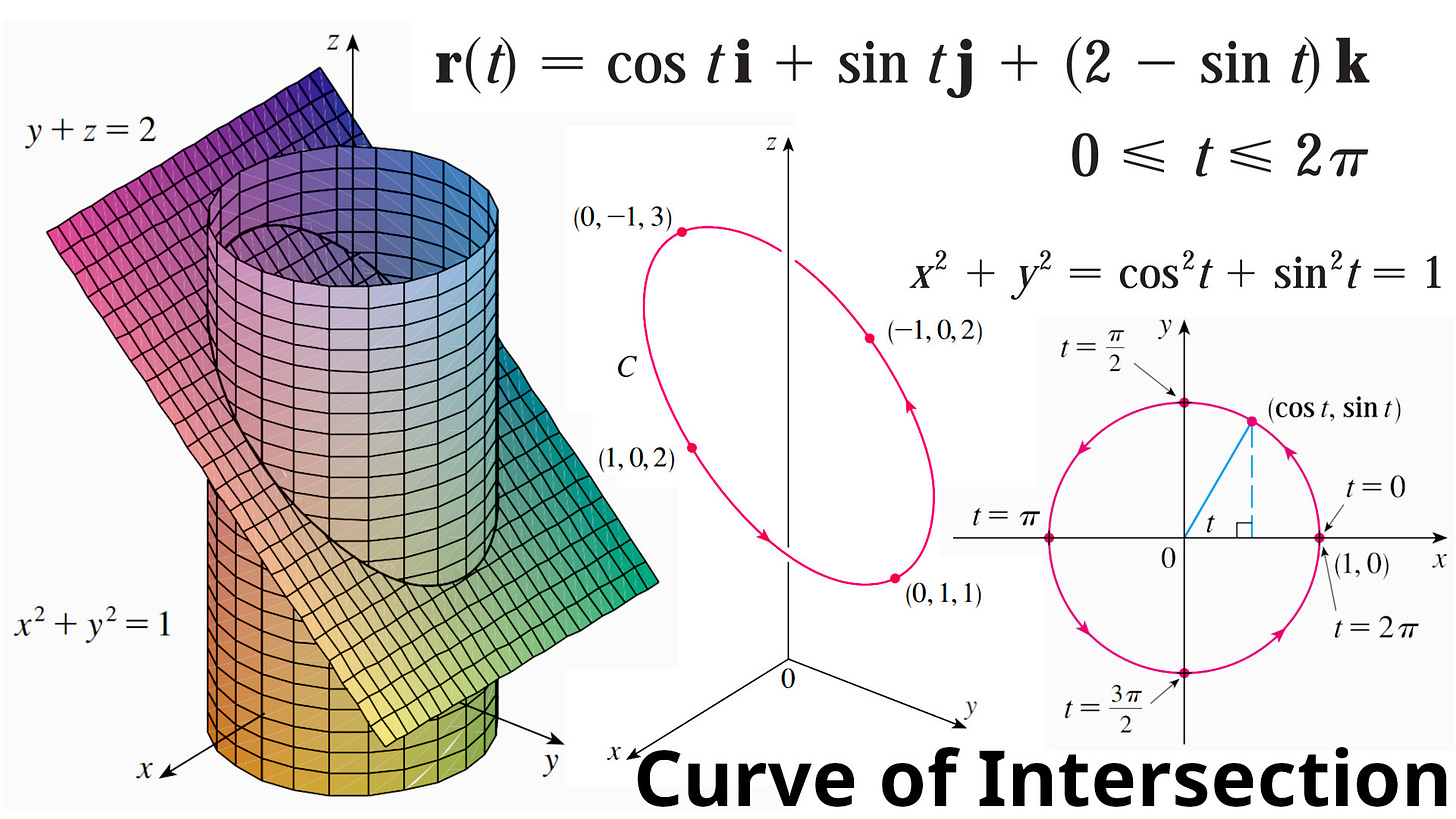
In this video I go over an example on determining the vector function of the curve of intersection between a vertical cylinder and a slanted plane. I first find an equation of the intersection by plugging the equation of the plane into the equation of the cylinder. I then determine 4 points of intersection and manually graph it out, obtaining an ellipse. Projecting this ellipse onto the x-y plane obtains a unit circle of radius 1. By using the Pythagorean Identity, I obtain parametric equations of the circle as trigonometric functions for x and y. By plugging the y parametric equation into the plane equation, we obtain the z parametric equation. From here we can combine the parametric equations into a vector function. Note that earlier in the video, I also graphed the plane and cylinder in GeoGebra 3D graphing calculator: https://www.geogebra.org/calculator/v7ecchdb
#math #vectorfunctions #geogebra #science #calculus
Timestamps
Example 6: Curve of Intersection: 0:00
Graphing the cylinder and plane in GeoGebra: 0:20
Equation at intersection: 1:23
2 Points of intersection when x = 0: 2:37
2 Points of intersection when x = +/- 1: 5:13
Graphing out points of intersection: 7:23
Better illustration of the intersection points from my Calculus book: 9:50
Projection of the intersection curve onto x-y plane is a circle: 10:56
Getting parametric equations of a circle via the Pythagorean Identity: 11:46
Converting plane equation into trigonometric version: 13:26
Parametric equations for the intersection curve: 14:27
Corresponding vector equation of the intersection curve: 15:00
Arrows on the curve indicate how the curve is traced as the parameter t increases: 16:03
Parameter t is the angle going counterclockwise from the positive x axis: 17:16








Share this post