YouTube - Video notes - Video sections playlist - Vectors and the Geometry of Space playlist
In this video I show that if the dot or cross products are zero then neither vector has to be zero, but if BOTH the dot and cross products are zero then at least one of the vectors has to be zero. If the dot product is zero, then it just means the two vectors are perpendicular to each other. If the cross product is zero, then it just means the two vectors are parallel. But if both the dot and cross products are zero, then the only way for the two vectors to both be perpendicular and parallel is if one of the vectors is a zero vector.
Timestamps
Question 19: Dot product can be zero if neither vectors are zero: 0:00
Question 20: Cross product can be zero if neither vectors are zero: 1:53
Question 21: If both dot and cross products are zero, then one vector has to be zero: 3:28

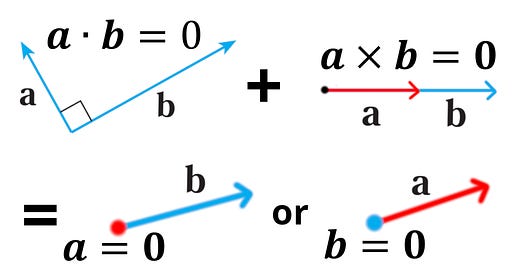


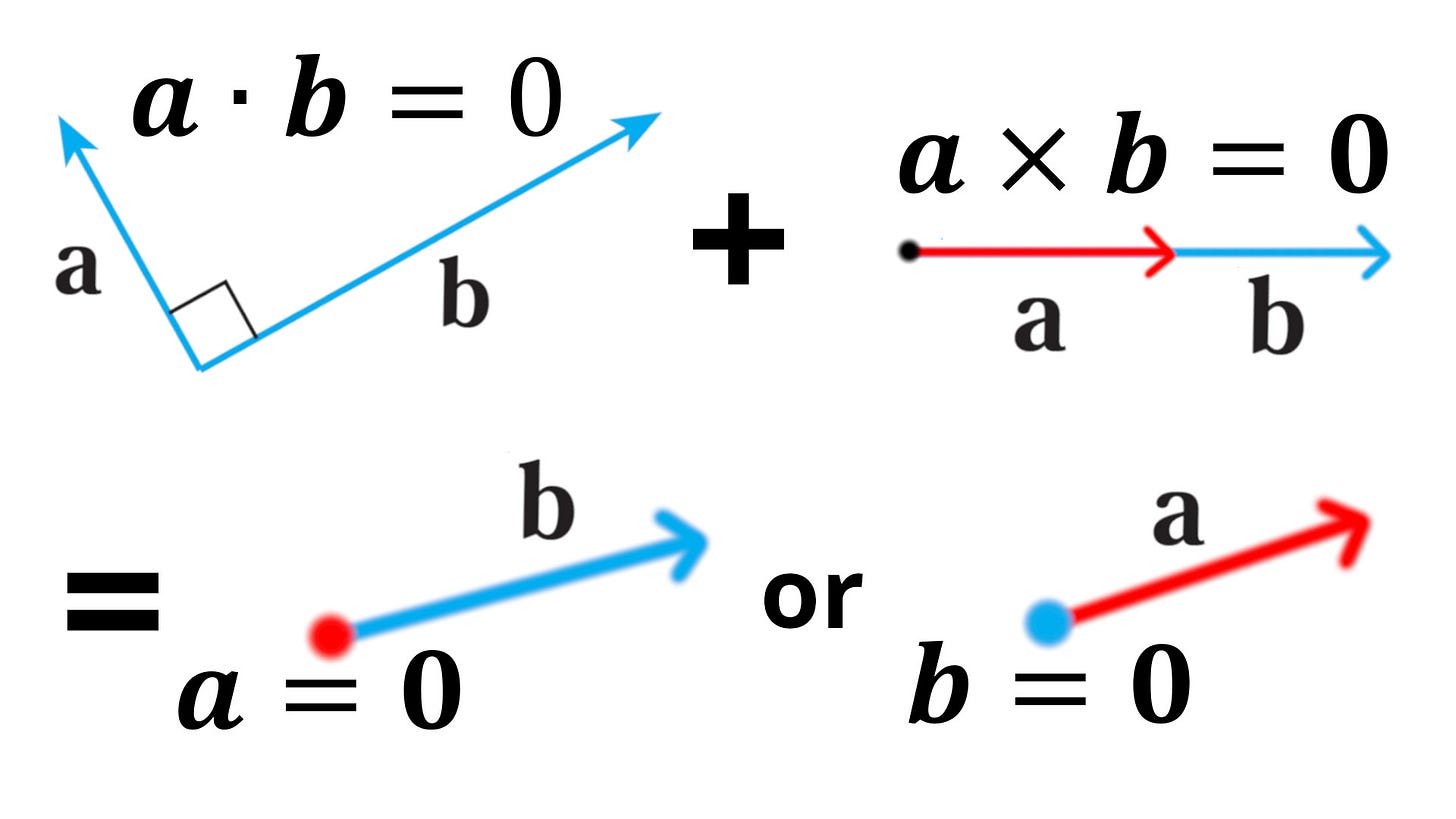








Share this post