YouTube - Summary - Notes - Playlist - Vector Functions playlist
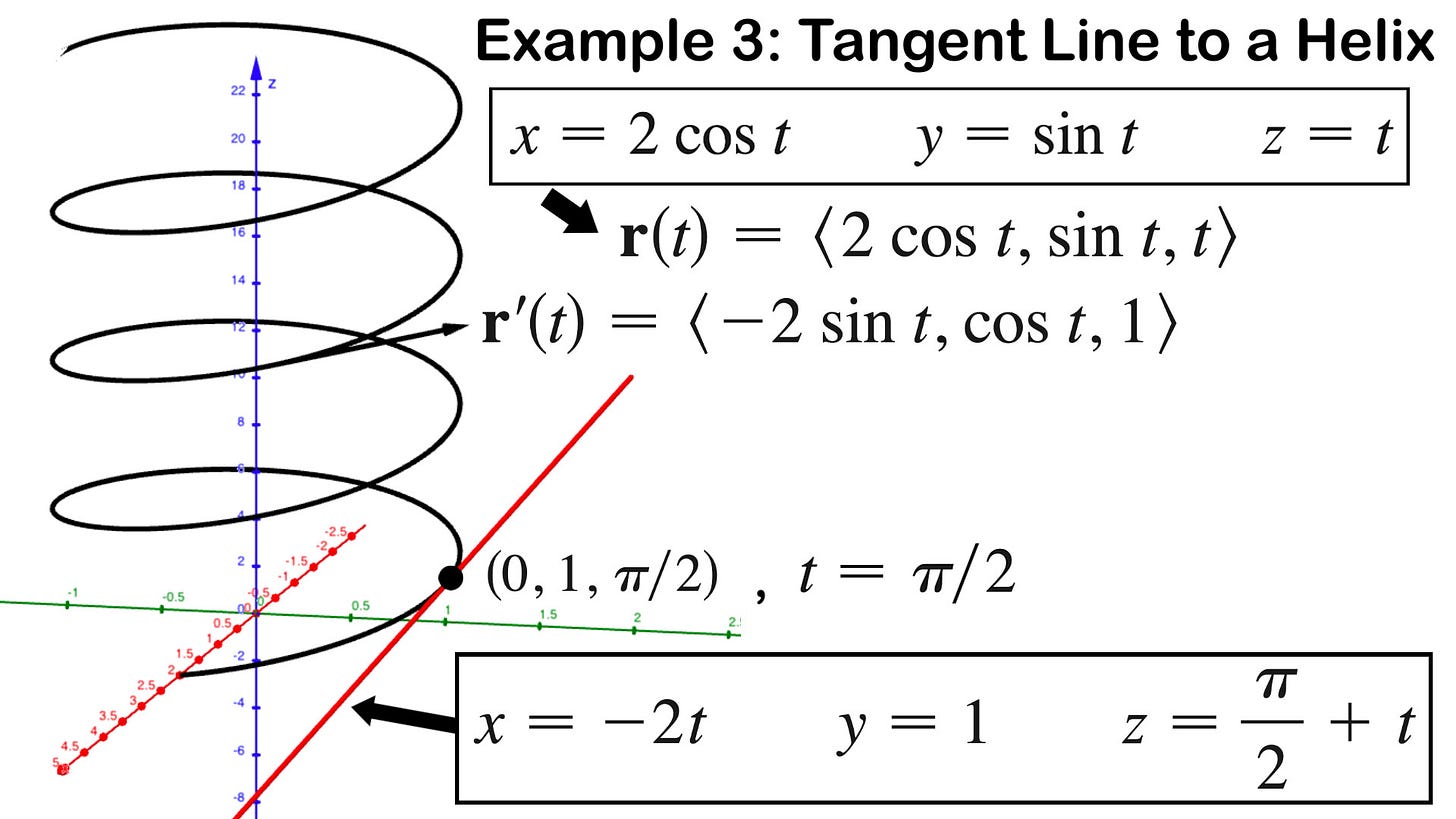
In this video I show how to obtain the parametric equations of a line that is tangent to a given point on a helix, whose parametric equations are also given. I first convert the helix parametric equations to its vector equation form and then take the derivative. I then obtain the parametric equations of our tangent line by using our given point and the derivative as the parallel vector. I also graph this out in GeoGebra’s amazing 3D graphing calculator, play around with it yourself! https://www.geogebra.org/3d/na9yk6pn
#math #helix #calculus #vectors #geogebra
Timestamps
Example 3: Tangent line to a helix: 0:00
Converting parametric equations to vector equation of the helix and taking the derivative: 0:32
Obtaining parameter value at our given point on the helix: 1:10
Derivative at our point on the helix: 3:11
Recap on the parametric equations of a line: 4:03
Obtaining the parametric equations of our tangent line: 5:33
Graph of the tangent line to the helix, and input equations for GeoGebra: 8:25
Graphing in GeoGebra’s 3D graphing calculator: 10:57