Watch on YouTube - Video notes - Video sections playlist - Vectors and the Geometry of Space playlist
In this video I discuss how to determine the distance between two lines for each of the 3 possible cases: intersecting lines, parallel lines, and skew lines (which don't intersect and are not parallel). If two lines intersect, their distance is zero, and we can equate their parametric equations and solve for each parameter. If there is no solution, then the lines do not intersect.
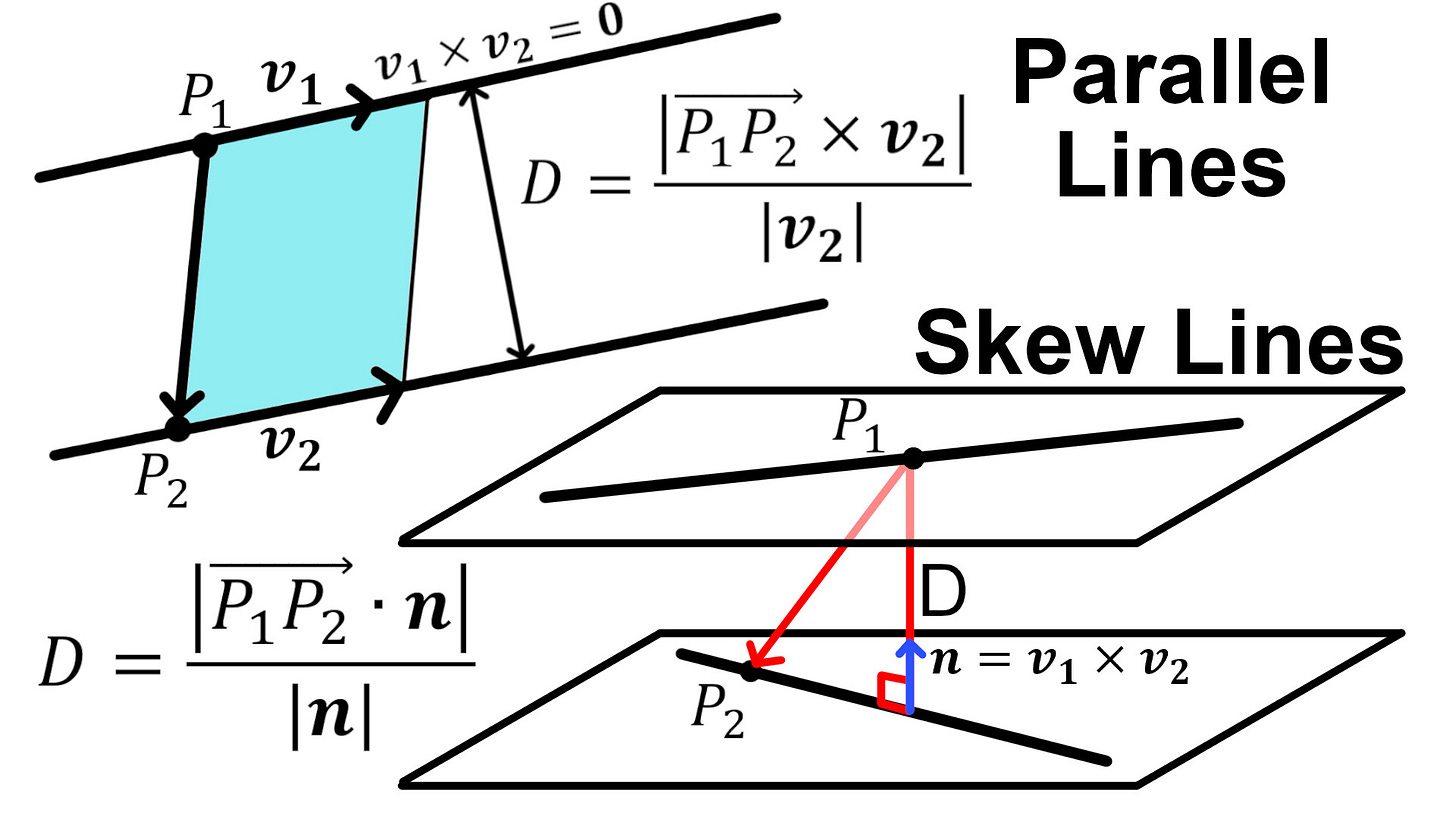
If two lines are parallel, then the cross product of their direction vectors is zero. We can solve for the distance between them using the same method as my earlier video by finding the height of the parallelogram spanned by their direction vectors.
If two lines are skew, then they don't intersect and are not parallel. In this case, the skew lines can be viewed as being on two parallel planes. We can thus use the formula for the distance between a point and a plane. The distance is just the scalar projection of a position vector connecting the two lines projected onto the normal vector, which is just the cross product of the direction vectors. Amazing stuff!
Timestamps:
Solution to Question 17 (c): Distance between two lines: 0:00
Case 1: Two lines intersect: Equate and solve for their parameters: 0:00
No solution if lines don't intersect: 2:32
Case 2: Two parallel lines: Cross product is zero: 2:38
Distance is the height of the parallelogram: https://youtu.be/-ie6FTLTH0E: 4:07
Distance = area of parallelogram divided by length of direction vector: 6:11
Case 3: Skew lines: Don't intersect and are not parallel: 6:59
GeoGebra: Skew lines can be viewed as being on two parallel planes: https://www.geogebra.org/calculator/kccatfbp: 7:07
Distance between a point and a plane formula: https://youtu.be/X3fpOF1bXEw: 8:17
Illustration of the method: 10:14
Distance is the scalar projection of a connecting vector onto the normal vector: 13:26
Distance Between Intersecting Lines, Parallel Lines, and Skew Lines