YouTube - Summary - Notes - Full video and playlist - MES Science playlist
In this video I go over a complete derivation of the cubic formula, which is the solution to the cubic equation. This proof utilizes the PQ substitution method, which I first demonstrate by solving for the quadratic formula. Using this substitution method, we can write the cubic equation in the form that we can then apply Vieta's substitution, which converts it into a quadratic equation. Now we can start going backwards and putting our solutions back into the previous substitutions. This involves a cube root, which gives 3 solutions and which we determine via the cube root of unity. Two of the solutions involve complex numbers, but fortunately the resulting 3 solutions in the cubic formula simply interchange the positive and negative signs of the complex numbers. While there is a ton of algebra, many terms repeat themselves so I just copied and pasted to save time. If you like math proofs, you'll love this one!
Note that I followed derivation by @blackpenredpen: https://youtu.be/ULsPhWmqhyc
Timestamps:
Intro: 0:00
Recap on Quadratic equation and formula: 0:40
Cubic Formula: 3:58
Derivation of Cubic Formula: 5:46
Step 0: Solve Quadratic Formula using PQ Substitution: 6:00
Step 1: Get rid of square power term using PQ Substitution: 12:44
Recap on Pascal's Triangle: 18:39
Applying the substitution: 20:22
Step 2: Apply Vieta's Substitution to obtain a quadratic equation: 28:04
Step 3: Find First Solution of y: 39:17
Step 4.1: Cube Root of Unity: 48:24
Complex factors are rotations in the complex plane: 1:00:10
Step 4.2: Find the other solutions for y: 1:05:26
Step 5: Put Everything Together to solve for x: 1:13:31
Double check and summary: 1:25:37
Outro: 1:27:27




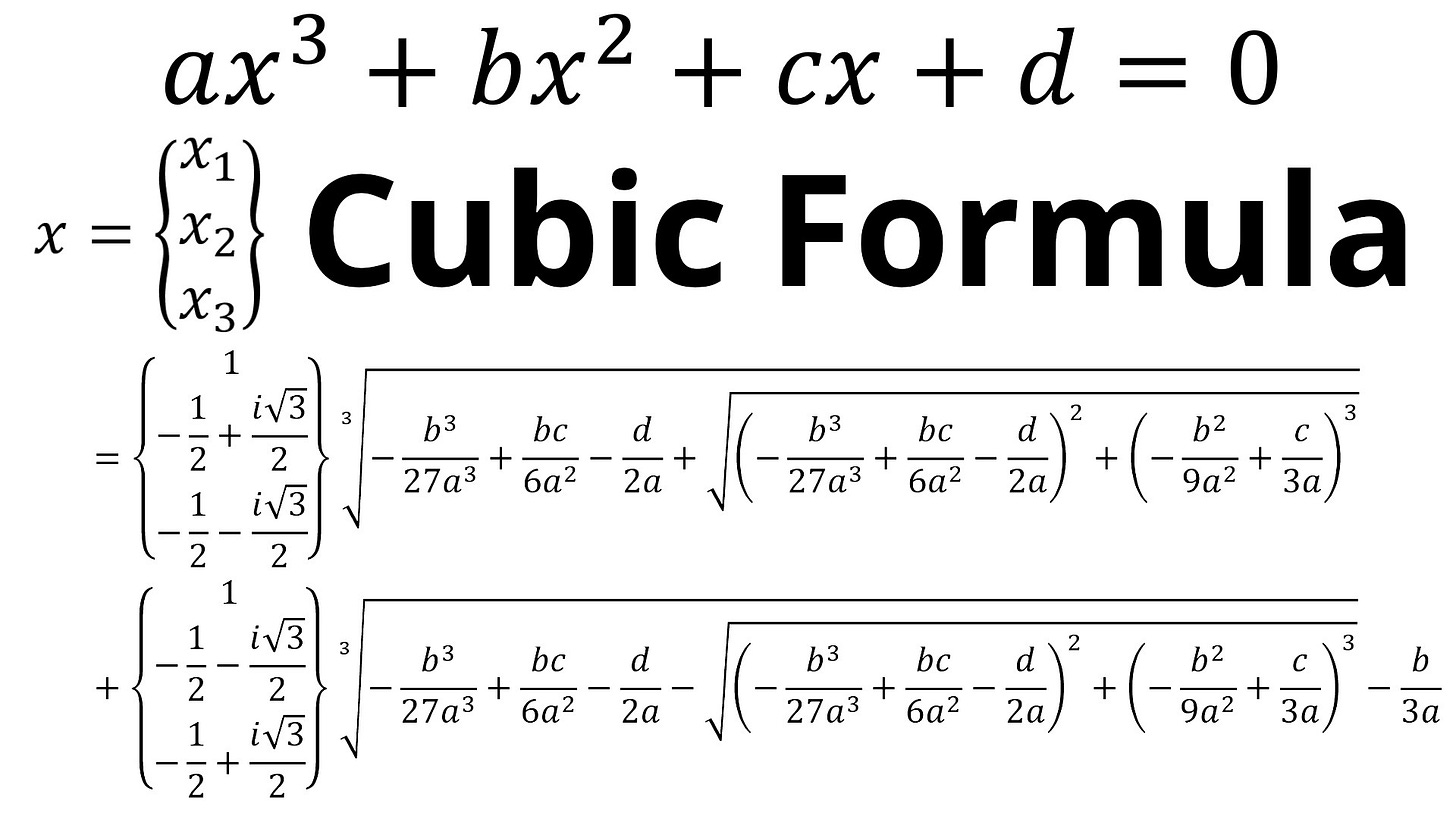








Share this post