YouTube - Summary - Notes - Playlist - Vector Functions playlist
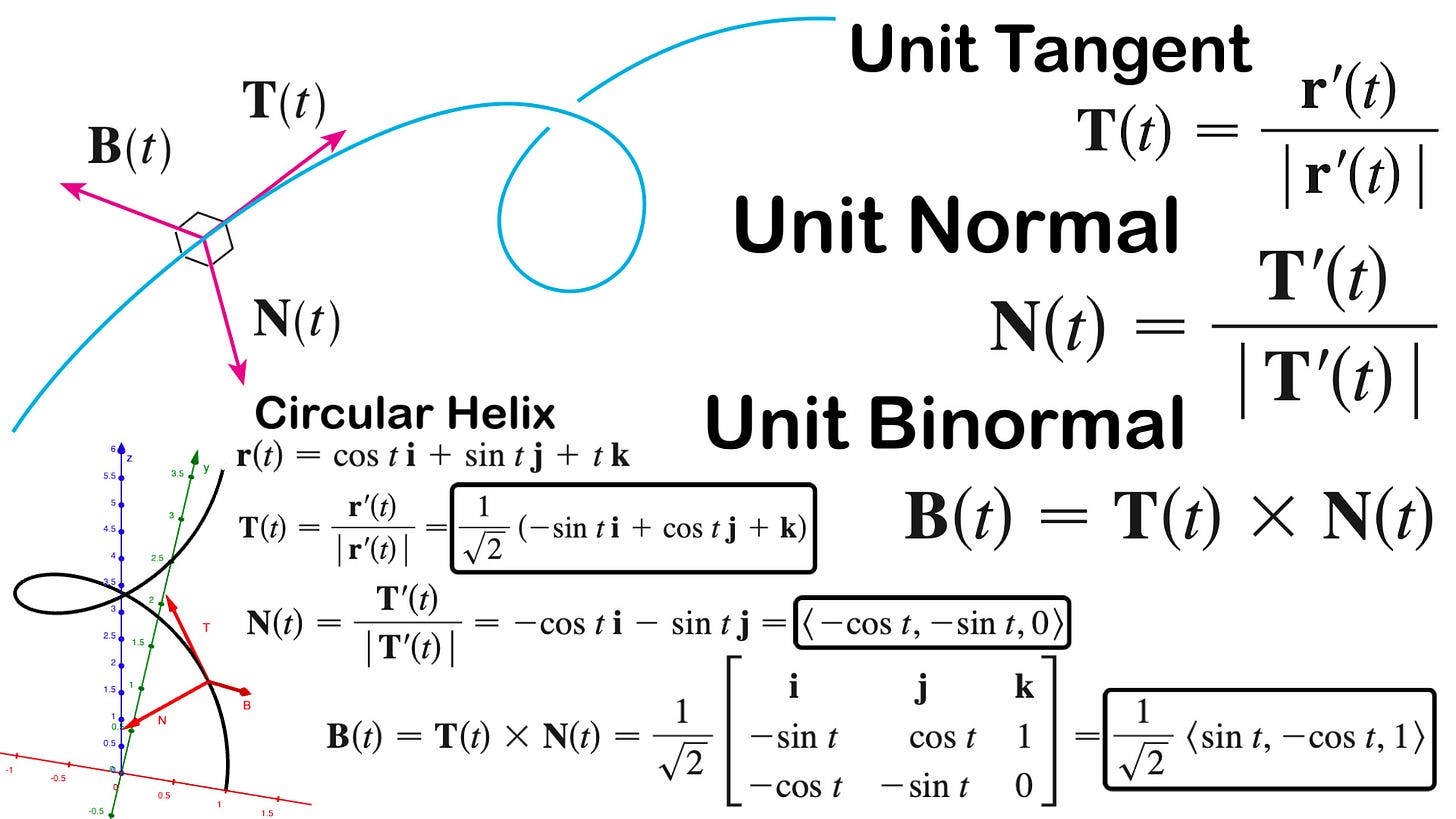
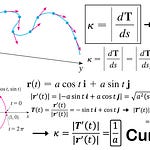
In this video, I go over the principal unit normal and binormal vectors of a space curve, which are both derived from the unit tangent vector. Since the unit tangent vector is a constant-length one, its derivative is perpendicular, thus it is a good candidate to select for our principal unit normal vector. Taking the cross product of the unit tangent vector and the unit normal vector yields the binormal vectors, all of which are perpendicular (or normal) to each other. These serve as good references for how a space curve bends and twists through space and time. I illustrate these through examples on a circular helix, as well as graphing it on the GeoGebra 3D graphing calculator. https://www.geogebra.org/3d/wyr5mysb
#math #vectors #calculus #geogebra #education
Timestamps
Principle Unit Normal Vector: Derivative of tangent vector divided by its magnitude – 0:00
Binormal vector: Cross product of principle unit normal with unit tangent vector – 3:11
Graphing the normal and binormal vectors: Lengths are 1 – 4:41
Example 6: Unit Normal and Binormal Vectors of a Circular Helix – 7:15
Solving for the unit normal vector – 13:34
Normal vector is pointing towards the z-axis – 15:31
Determining the binormal vector – 17:58
Solving the cross product to get the binormal vector – 22:53
Graphing the unit vectors on the circular helix – 23:18
Graph of the helix and its unit vectors with GeoGebra: https://www.geogebra.org/3d/wyr5mysb – 24:53
View from the top showing the unit normal vector pointing to the origin – 27:37